How to Find Square Root Without Calculator

Finding the square root of a number can be a daunting task, especially if you don't have a calculator in hand. But fear not, there are several methods you can use to find the square root of a number without a calculator. In this blog post, we'll go over several methods and provide external links for further explanations and examples. Also the square root is used to calculate the standard deviation and the standard deviation is used to calculate the confidence interval. So, both concepts are related and used in statistics, but for different purposes.

You can use our confidence interval calculator tool for free along with many other useful tools that dbcalculator offer including tax calculator, average calculator, tip calculator, age calculator, and more

Method 1: Prime Factorization

The first method we'll discuss is finding the square root through prime factorization. This method involves breaking down a number into its prime factors and then using those factors to find the square root.

To start, we'll need to find the prime factors of the number we're trying to find the square root of. Once we have the prime factors, we'll group them into pairs of two and take the square root of each pair. The final square root will be the product of all the square roots of each pair.

For example, let's say we want to find the square root of 144. The prime factors of 144 are 2^4 x 3^2. To find the square root, we'll take the square root of each pair (2^2 x 3^1). The final square root of 144 is 12.

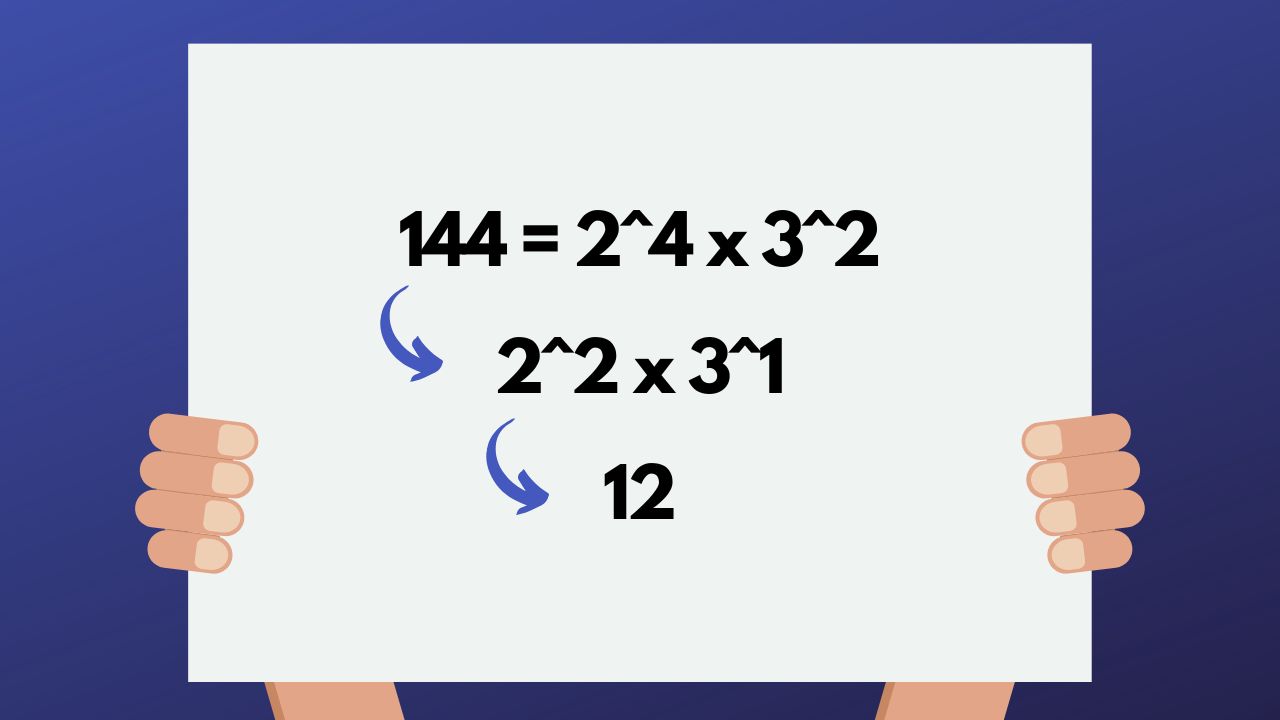
For a more in-depth explanation and examples of finding the square root through prime factorization, check out this link: 

Method 2: Long Division

Another method for finding the square root is through long division. This method involves dividing the number we're trying to find the square root of by a series of numbers until we find the closest match.

To start, we'll divide the number we're trying to find the square root of by a number that's close to the square root. We'll then make adjustments until we find the closest match. Once we find the closest match, we'll divide that number by 2 to find the final square root.

For example, let's say we want to find the square root of 121. We'll start by dividing 121 by 11 (which is close to the square root of 121). We'll then make adjustments until we find the closest match. In this case, the closest match is 11. We'll then divide 11 by 2 to find the final square root of 11.

For a more in-depth explanation and examples of finding the square root through long division, check out this link:

Method 3: Estimation

The third method we'll discuss for finding the square root is through estimation. This method involves finding an approximate square root by comparing it to a number we already know the square root of.

To start, we'll find a number that's close to the number we're trying to find the square root of and compare it to a number we already know the square root of. We'll then make adjustments until we find the closest match.

For example, let's say we want to find the square root of 15. We'll start by comparing 15 to 16 (which is a perfect square and we know the square root is 4). We'll then make adjustments until we find the closest match. In this case, the closest match is 3.5.

For a more in-depth explanation and examples of finding the square root through the estimation, check out this link:

finding the square root of a number without a calculator, including prime factorization, long division, and estimation. Each method has its own unique approach and can be useful in different situations.

It's important to note that while these methods can be used to find the square root of a number, they may not always provide the exact answer. However, they can still be useful in providing a close approximation of the square root.

It's also important to practice and become familiar with these methods. The more you practice, the more comfortable you will become with them, and the easier it will be to find the square root of a number without a calculator.

In summary, finding the square root of a number without a calculator may seem daunting, but with the methods discussed in this blog post, it can be done with ease. Remember to practice, use external resources for further explanations and examples, and always keep an open mind when trying different methods. Happy calculating!