A beginner’s guide to calculating standard deviation of sample/ population data values

Standard deviation plays an important role in the field of mathematics and statistics in determining the dispersion of data and whether the standard deviation is very necessary for the field of statistics for the separation of data set values on the graph. 

As the higher standard deviation value indicates the data points are spread out which shows the dispersion of the data set is very high. It also provides detailed information about the data points, and how much the points deviate from the mean line in the graph. 

Moreover, the value of standard deviation gives information on how to close the mean, if the value of standard deviation is low then it indicates the values tend to close the mean of the data set while a large value of standard deviation shows that the values are away from the mean and spread in a wide range.

Determining the value of the standard deviation for the sample/population data set is a difficult task. Also, many people are worried about determining the exact value of the standard deviation. 

Now you don’t worry about that, in this article I will provide a step-by-step guide to finding the standard deviation using a manual method and also provide advanced techniques to find the solution of standard deviation by using an advanced online tool.

What is standard deviation?

Standard deviation is a statistical measure that determines the amount of variation and separations of the data set values around their means of the data set. It is also known as the expected value of the data set. 

Formulas of standard deviation

Standard deviation formula is changed due to the state of the data such as the sample data set and population data set. A population data set refers to the values of the entire values of given data whether a sample is the subset of the population values of the given data values.

Formula For Population Data Set

The formula of standard deviation for the population data set is stated as, 

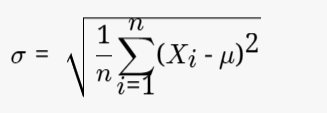
Where,

• σ = standard deviation of a population data set
• n = total number of values in a data set
• Xi = ith-value in the data set of population
• µ = mean of population

Formula For Sample Data Set

However, the mathematical formula of standard deviation for the sample value of data set is defined as, 

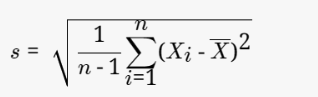
Where, 

• s = represents standard deviation of the sample data set
• n = sample size of data set 
• Xi = ith-value in the data set of population
• X = sample mean of a data set

Calculate Standard Deviation By Manual Method

Standard deviation is found by simply putting the values in the formulas and applying the mathematical techniques to perform the calculations. For the solution of standard deviation, we need a sample/population data set.

To find the standard deviation follow the below steps.

• First, write the data set in ascending order.
• Find the mean of the data, dividing the sum of all data set values by the total number of elements present in a data set. 
• Thirdly, calculate the sum of the squares of the difference of the data value and mean of a data set.
• Then, divide the sum of squares divide with the number of the data according to the sample/population data set value.
• Now, put the values in the standard deviation formula and get the final results.

Here we perform the manual examples to determine the solution of standard deviation using its formula.

Example

Find the standard deviation of the below sample data set,

{14, 15, 8, 24, 11, 18}.

Solution

Step 1: First, arrange the data in ascending order and find the mean of the data.

Ascending order = 8, 11, 14, 15, 18, 24

Mean = 14+15+8+24+11+18/6 

           = 90/6 = 15

Step 2: Find the sum of the squares of the difference of each data set value by the mean of the data set.

∑ i=1 n=6 (xi - x̅)2 = (x1 - x̅)2+ (x2 - x̅)2+ (x3 - x̅)2+ (x4 - x̅)2+ (x6 - x̅)2+ (x7 - x̅)2

            = (8- 15)2+ (11 - 15)2+ (14 - 15)2+ (15 - 15)2+ (18 - 15)2+ (24 - 15)2

            = (-7)2+ (-4)2+ (- 1)2+ (0)2+ (3)2+ (9)2

            = 49 + 16 + 1 + 0 + 9 + 81

∑ i=1 n=6 (xi - x̅)2 = 156

Step 3: Now put the values in the standard deviation sample formula.

n = 6, ∑ i=1 n=6 (xi - x̅)2 = 156

s = √1/n−1​ ∑i=1n (xi - x̅)2

   = √1/6−1​ (156)

   = √​ 156 /5

  = √​ 31.2

s = 5.58

Advanced Techniques To Determine Standard Deviation

To determine the value of the standard deviation by manual methods or using its formula and applying algebraic techniques is a difficult or time-consuming task. The manual method takes more time and there are chances in the calculation of the answer that becomes the reason for the wrong answer.  Where we provide advanced techniques to find the standard deviation quickly and error-free by using online tools.

There are many sites to give the solution of the standard deviation with the help of online free mathematical tools but we note that standarddeviationcalculator.io is the best-ever website that provides the solution of this type of problem accurately and quickly with a single click. This website makes solutions faster and error-free with detailed steps or provides graphical information. 

What is standarddeviationcalculator.io?

Standarddeviationcalculator.io is a free website with many online free statistical tools that make solving different statistical problems easier. This site has many best tools such as (A chi-square calculator, Mean calculator, Mode calculator, Median calculator, Anova calculator, and Z-score calculator) for solving different statistical problems using the group data and data set values such as the sample/population data set.

While we noted that the standard deviation calculator of this website is the best tool that helps to evaluate the value of the standard deviation for sample/population data values. This calculator makes the calculation easier or faster than long manual calculations and saves your precious time. 

How to Find standard deviation using standarddeviationcalculator.io?

Standarddeviationcalculator.io calculates the standard deviation with a single click by just entering the values of the sample or population data set. It also provides detailed steps of every problem and provides the graph of every data set value rather than sample/population data values given in input fields. No matter how the data set length is large or small.

Follow the below steps to find the values of standard deviation using standarddeviationcalculator.io. 

• Enter the value of the given input fields and values are separated with commas.
• Select the data type (sample/population) from bullet points.
• Press the calculate button to find your required values.
• See your answer along the right side of the input selection with detailed steps and a graph of your data set.

 

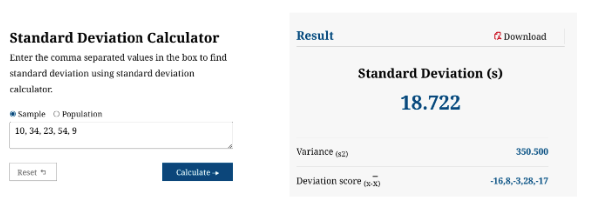
Here we solve the problem with the use of standarddeviationcalculator.io.

Example:

Find the solution of the given data set by using sample and population selection.

Solution:

Step 1: Put the values in the given data set and select the sample option.

Step 2: After pressing the calculate button and get the desired results.

Conclusion:

Standard deviation is a valuable contribution to statistics and measures to know the spread of data around the mean. While manual calculation methods exist, they can be time-consuming and have chances of error. Moreover, online calculators overcome this problem like standarddeviationcalculator.io which offers a fast and accurate alternative. This website provides step-by-step solutions and graphical representations that make it a user-friendly resource for anyone who needs to find the standard deviation. 

By understanding standard deviation and using online tools like standarddeviationcalculator.io, you can get remarkable results in your data and make your decision clever.